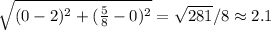Question

It would be really helpful if anyone solved this for me !!!! It's differentiation.

Answer 1

Determine point A:

`y(x)=(10)/(2x+1)-2\\(10)/(2x+1)-2=0\implies x=2`

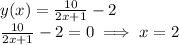
so A(2,0)

Find the function for the tangent:

`(dy)/(dx)=-(-20)/((2x+1)^2)`

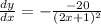
the tangent function is a line

`y=ax + b = (dy)/(dx)|_A\cdot x + b\\`

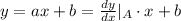
(with slope being the derivative evaluated at point A(2,0))

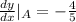`(dy)/(dx)|_A=-(4)/(5)` so a=-4/5.

Determine b by using what we know about A:

`y=-(4)/(5)x+b\\0=-(4)/(5)\cdot 2+b\implies b=(8)/(5)`

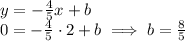
so the function is

`y = -(4)/(5)x+(8)/(5)\\5y + 4x = 8`

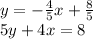
(i) this is demonstrated above

(ii) distance AC: we know A(2,0) and C(0,5/8), the distance is:

`\sqrt{(0-2)^2+((5)/(8)-0)^2}=√(281)/8\approx 2.1`