Question

3. The data set shows the number of practice throws players in a basketball competition made and the number of free throws they made in a timed competition.

(a) Use technology to find the equation and coefficient of determination for each type of regression model. Use the number of practice throws for the input variable and the number of free throws for the output variable. Round all decimal values to three places.
(b) Which model best fits the data set? Explain.

Answer 1

The exponential model best fits the data set.

Solution-

x = input variable = number of practice throws

y = output variable = number of free throws

Using Excel, Linear, Quadratic and Exponential regression model were generated.

The best fit equation and co-efficient of determination R² are as follows,

Linear Regression

`y=2.155x+0.391,\ R^2=0.903`

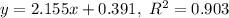
Quadratic Regression

`y=0.096x^2+0.713x+3.803,\ R^2=0.948`

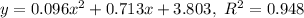
Exponential Regression

`y=4.625e^(0.141x),\ R^2=0.951`

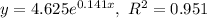
The value of co-efficient of determination R² ranges from 0 to 1, the more closer its value to 1 the better the regression model is.

Now,

`R^2_(Linear)< R^2_(Quadratic)< R^2_(Exponential)`

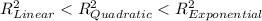
Therefore, the Exponential Regression model must be followed.