1. Point O (the point of intersection of diagonals) divides two diagonals AC and BD into parts that are proportional:
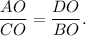
Then

2. Consider triangle ABO. The area of this triangle is
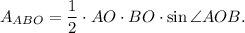
3. Consider triangle COD. The area of this triangle is
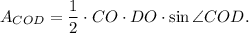
Since
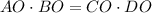 and angles AOB and COD are congruent as vertical angles, then
and angles AOB and COD are congruent as vertical angles, then

Answer: 6 sq. in.