(a) Take any point
 in the plane
in the plane
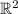 . To reflect this point in the
. To reflect this point in the
 -axis, you need to negate the
-axis, you need to negate the
 -component, so that
-component, so that
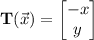
(b) This can be done easily by choosing
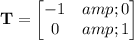
as
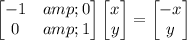
(c) Computing
 (very easy since it's diagonal) returns the identity matrix
(very easy since it's diagonal) returns the identity matrix
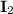 , which as a linear transformation returns whatever it is applied to. Geometrically, we're applying the same reflection twice, which returns the original vector to its starting value/position in the plane.
, which as a linear transformation returns whatever it is applied to. Geometrically, we're applying the same reflection twice, which returns the original vector to its starting value/position in the plane.
(d) If
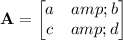
then
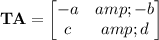
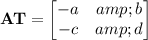

Multiplying
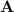 by
by
 on the left is equivalent to negating the first row of
on the left is equivalent to negating the first row of
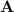 , and on the right to negative the first column of
, and on the right to negative the first column of
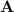 . The third product is equivalent to negating the antidiagonal.
. The third product is equivalent to negating the antidiagonal.