Substitute 136.5 for y.
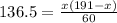
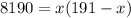
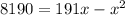
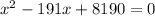
Compare this equation with
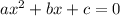
a = 1, b = - 191, c = 8190
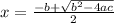 or
or
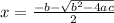
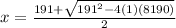 or
or
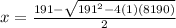
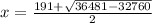 or
or
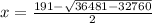
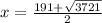 or
or
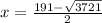
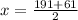 or
or
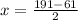
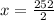 or
or
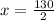
x = 126 or x = 65
Hence, the points on the curve are (65, 136.5) and (126, 136.5).
The width of the air space is the distance between these points.
Width =
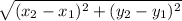
=
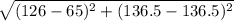
= 126 - 65
= 61
Hence, width of the air space is 61m.