The fourth or the D) Option is correct.
To find the new induced matrix via a scalar quantified multiplication we have to multiply the scalar quantity with each element surrounded and provided in a composed (In this case) 3×3 or three times three matrix comprising 3 columns and 3 rows for each element which is having a valued numerical in each and every position.
Multiply the scalar quantity with each element with respect to its row and column positioning that is,
Row × Column. So;
(1 × 1) × 7, (2 × 1) × 7, (3 × 1) × 7, (1 × 2) × 7, (2 × 2) × 7, (3 × 2) × 7, (1 × 3) × 7, (2 × 3) × 7 and (3 × 3) × 7. This will provide the final answer, that is, the D) Option.
To interpret and make it more interesting in LaTeX form. Here is the solution with LaTeX induced matrix.
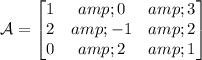
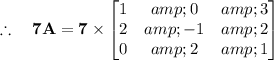
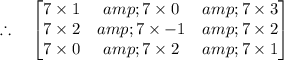
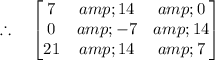
Hope it helps.