Answer:
The value of x lies between 20 and 40 and value of y lies between -20 and 10
Explanation:
We are given that
 ....(1)
....(1)
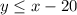 ...(2)
...(2)
First we convert inequality equation into equality equation to find the solution of the given system of inequality equation.
Therefore, we can write as
 ...(3)
...(3)
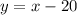 ...(4)
...(4)
Adding equation (3) and (4) we get
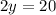
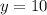
Substitute y=10 in equation (3) we get
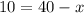

(30,10) is the intersect point of two equation.
Put x=0 in equation (3)

Substitute y=0 in equation (3)
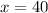
Substitute x=0 in equation (4)

Substitute y=0 in equation (4)
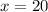
Substitute x=0 and y=40 and in equation (1)
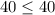
Hence, the equation is true.Therefore, the shaded region below the line.
Substitute x=0 and y=-20 in equation (2)
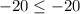
The equation is true. Hence, the shaded region is below the line.
Hence, the value of x lies between 20 and 40 and value of y lies between -20 and 10.