Answer-
The area after 11 years will be 2225.28 km²
Solution-
This can be represented as exponential decreasing function,

Where,
- a = starting amount
- r = rate
- t = years
Putting the values,
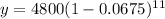
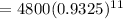
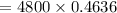
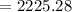
Therefore, at this rate the area of the forest after 11 years will be 2225.28 km².