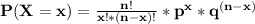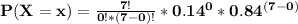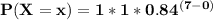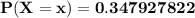Question

According to a recent​ study, 14% of u.s. drivers are uninsured. a random sample of seven drivers was selected. what is the probability that none of these drivers are​ uninsured?

Answer 1

Answer: The probability that none of the drivers are uninsured is 0.3479 or 34.79%.

We can answer this question as follows:

We use the binomial distribution formula in order to find the probability.

The formula is as follows:

`\mathbf{P(X=x) =_(n)^(x)\textrm{C}*p^(x)*q^((n-x))}`

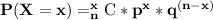
where

n is the total number of trials = 7

x is the number of successes among the trials = 0

p refers to the probability of success = 0.14

q refers to the probability of failure = 1-p =
`1-0.14 = 0.86`

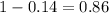
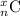`_(n)^(x)\textrm{C}` is the combination of choosing x items from a total of n items

Substituting the values we get

`\mathbf{P(X=x) =(n!)/(x!*(n-x)!)*p^(x)*q^((n-x))}`

`\mathbf{P(X=x)=(7!)/(0!*(7-0)!)*0.14^(0)*0.84^((7-0))}`

`\mathbf{P(X=x)= 1*1*0.84^((7-0))}`

`\mathbf{P(X=x)= 0.347927822}`