Question

SOME ONE HELP ME I REALLY NEED A SOLUTION FOR THIS PROBLEM WITH A CLEAR EXPLANATION

Answer 1

I'm going to answer this question using logic. Let x be Jenny's favorite number. We are going to square root this number,
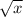`√(x)` and then multiply it by
`√(2)`.

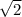This product needs to be an integer. How is that obtainable? To be an integer, we need to get rid of the nasty
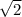`√(2)` part. The only way I can think of to get rid of it, is to multiply it by
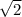`√(2)`, because
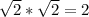`√(2) *√(2) = 2`. Thus we have some conditions we need to fulfill when choosing Jenny's favorite number.

When we take the square root of Jenny's favorite number, x, it must contain a perfect square and a 2 in its prime factorization. For example, 8 works because 8 = 2 x 2 x 2, or 2² x 2.

You notice 8 is made up of a perfect square multiplied by 2. So when we take the square root of 8, we get:

`√(8) = \sqrt{2^(2)*2 } = \sqrt{ 2^(2) }*√(2) = √(4) *√(2) = 2*√(2)`

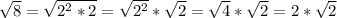
So 8 is the same thing as
`2√(2)`

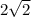
So when we multiply this by
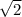`√(2)`, we will get an integer! So as long as Jenny's favorite number consists of a perfect square and two in its prime factorization, we will have an integer!

So possible choices are: 2,8,18.

Why does 18 work? Because
`√(18) = √(9)* √(2) = 3√(2)`

When we multiply this by
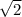`√(2)`, we get 6, which is an integer.

b) Suppose instead of multiplying by
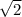`√(2)`, we divided by
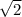`√(2)`. Is the resulting quotient still an integer?

YES, because we can get rid of the
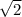`√(2)` part by dividing by
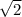`√(2)` as well. This leaves only the "perfect square" part left in our square root, and obviously a perfect square is an integer when we square root it.

I hope that made sense! (⌐■_■)