Question

Sitting on a park bench, you see a swing that is 100 feet away and a slide that is 60 feet away. The angle between them is 30°. What is the approximate distance between the swing and the slide? A. 120 feet B. 57 feet C. 53 feet D. 147 feet

Answer 1

its 57 on apex. good luck

Answer 2

A. 120 feet

Step-by-step explanation:

Let A = the location of the slide and B = the location of the swing. C = your location.

The angle between A and B, ∠CBA, is 30°.

The way I have this set up has the 30° angle across from the 60 ft side. Using the Law of Sines to solve for ∠BAC,

`(sin(30))/(60)=(sin(A))/(100)`

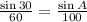
Cross-multiplying gives us

100(sin 30) = 60(sin A)

Divide both sides by 60:

(100(sin 30))/60 = (60(sin A))/60

0.833333 = sin A

5/6 = sin A

To find the measure of angle A, take the inverse sine:

sin⁻¹(5/6) = A

56.4 = A

This gives us two of the three angles; this leaves the third angle, ∠BCA, to be

180-(30+56.4) = 180-86.4 = 93.6

Using the Law of Sines to find side AB, we have

`\frac{sin{30}}{60}=(sin(93.6))/(c)`

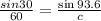
Cross multiplying, we have

b(sin 30) = 60(sin 93.6)

Divide both sides by sin 30:

(b(sin 30))/(sin 30) = (60(sin 93.6))/(sin 30)

b = 119.76 ≈ 120