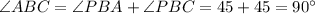Answer:
See Below.
Explanation:
In the given figure, AP = BP = PC.
And we want to prove that ∠ABC is a right angle.
Since AP = BP and BP = PC, we can create two isosceles triangles: ΔAPB and ΔCPB.
By the definition of isosceles triangles, in ΔAPB, ∠PAB and ∠PBA are equivalent. Let the measure of each of them be x°.
Likewise, in ΔCPB, ∠PCB and ∠PBC are equivalent.
And since AP = BP = PC, each of the angles∠PCB and ∠PBC will also be equivalent to x°.
And since the sum of the interior angles of a triangle total 180°, we acquire:
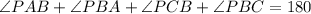
Since they are all equivalent:
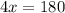
Hence:
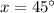
∠ABC is the sum of ∠PBA and ∠PBC, each of which measures 45°. Hence: