Question

1) Write an absolute value equation that is reflected, vertically shifted 2/3 units down and 1/2 units to the right.

2) Write an absolute value equation with a horizontal shift 4 units to the right.

Answer 1

Question 1) Write an absolute value equation that is reflected, vertically shifted 2/3 units down and 1/2 units to the right.

Answer 1):

We know that absolute function is given by y=|x|

reflection happens when we multiply by negative sign so we get

y=-|x|

To get vertical shift down, we subtract so new equation is

y=-|x|-2/3

To get right shift by h unit, we replace x by (x-h) so the new equation is

y=-|x-1/2|-2/3

Hence final answer is

`y=-\left|x-(1)/(2)\right|-(2)/(3)`

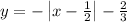
Question2) Write an absolute value equation with a horizontal shift 4 units to the right.

Answer:

We know that absolute function is given by y=|x|

To get horizontal right shift by h unit, we replace x by (x-h) so the new equation is

`y=|x-4|`

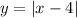
Hence final answer is
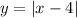`y=|x-4|`.