Answer:
The answer is NO SOLUTION
Explanation:
Firstly, we have to subtract 60 from each side of the equation:
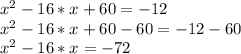
Then, to complete a square of a binomial, the rules are:
Let
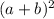 a square of a binomial, its expansion is:
a square of a binomial, its expansion is:
- square of the first term
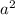
- twice the product of the two terms
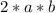
- square of the last term
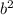
So,
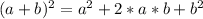
Then , we have the first term that is
 and the second term is
and the second term is
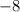 because
because
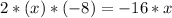 .
.
Therefore, we need to add 64 (=
 ) from each side of the equation:
) from each side of the equation:

Finally, we know that it doesn't exist negative square root in the real number group, so there are not "x" values to solve the equation.