Answer:
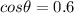
Step-by-step explanation:
In the given triangle, perpendicular distance is 12 units and the hypotenuse of the triangle is 15 units. Let b is the base of the triangle. It can be calculated using the Pythagoras theorem as :
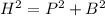
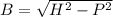
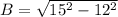
B = 9 units
Now we need to find the value of
 . Using trigonometric identities as :
. Using trigonometric identities as :
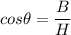
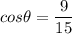
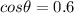
So, the value of
 is 0.6. Hence, this is the required solution.
is 0.6. Hence, this is the required solution.