Question

Select from the drop-down menus to correctly complete the proof.

To prove that 2√⋅7 is irrational, assume the product is rational and set it equal to ​ ab ​, where b is not equal to 0. Isolating the radical gives ​ 2√=a7b ​ . The right side of the equation is (irrational, rational). Because the left side of the equation is (irrational, rational), this is a contradiction. Therefore, the assumption is wrong, and the product is (rational, irrational).

Answer 1

Rational

Irrational

Irrational

I just took the test . You're Welcome. Don't let anyone confuse you these are 100% right.

Answer 2

Answer: Rational, irrational and irrational.

Explanation:

According to the question, We have to prove that 2√7 is irrational.

Let us assume 2√7 is a rational number.

Then, by the property of rational number both 2 and √7 must be rational.

Since, we know that 2 is a rational number( because it is an integer).

Now, Let √7 is also a rational number so that √7=a/b where b≠0 and a and b are distinct numbers.

√7=a/b⇒√7a=b⇒
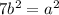`7b^2=a^2` ----------(1) (by squaring both sides)

⇒7 is a multiple of
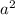`a^2` ⇒ 7 is a multiple of a. --------(2)

So, we can write a=7k, where k is any number.

From equation (1)
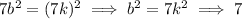`7b^2=(7k)^2\implies b^2=7k^2\implies 7` is a multiple of
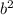`b^2`⇒7 is a multiple of b ----------(3)

From equation (1) and (2) 7 is multiple of both a and b.

⇒a and b can not be distinct. Therefore, our assumption is wrong and √7 is a irrational number⇒2√7 is a irrational number.