Question

Which are the factors of x^2-4x-5

Answer 1

`x^2-4x-5 =\\\\x^2+x-5x-5=\\\\x(x+1)-5(x+1)=\\\\(x-5)(x+1)`

Answer 2

Easy. Given expression in current equation.


`\mathbf{x^2 - 4x - 5}`

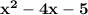
First break those following expressions in the current equation into grouped form, as to, relate the value as completely equal and not altering the actual expression. So;


`\mathbf{(x^2 + x) + (- 5x - 5)}`

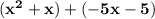
Factor out the variable of 'x' from the expression of
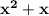
`\mathbf{x^2 + x}`. We are getting by factoring 'x';
`\mathbf{x (x + 1)}`.

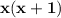
Factor out the numbered negative value of '5' from the expression of
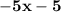
`\mathbf{- 5x - 5}`. We are getting by factoring '5';
`\mathbf{- 5 (x + 1)}`.


`\mathbf{\therefore \quad x (x + 1) - 5 (x + 1)}`

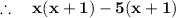
Factor out the expression as a common term on both side, to obtain the final answer, that is,
`\mathbf{(x + 1)}`


`\boxed{\mathbf{\underline{(x + 1)(x - 5)}}}`

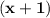
Hope it helps.