Question

OVERDUE 3 DAYS LATE

HURRY HURRY HURRY Hurry! the table shows the input and output of a function. Input 3 5 4 7 Output 6 11 11 21
(a) Explain what makes this set of data a function?.

(b) What could cause this set of data to not be a function? Provide a specific example to support your statement and explain thoroughly.

(c) Write an equation, in function notation, that would fit the inputs and outputs in the table. Show work that proves your equation is true for the given data.

Answer 1

Ans(a):

We know that a function can't have repeated x-values.

In given table we see that there i no repeating x-value. That's why the given table represents function.

Ans(b):

We know that a function can't have repeated x-values.

So if in given table we see any repeating x-value then that may cause the given data set to not be a function.

like if we have 3, 4, 3, 11 in the input then it will not be a function.

Ans(c):

If we graph the given points then they appear to be in the shape of cubic function so we can use standard formula of cubic function which is

`y=ax^3+bx^2+cx+d`

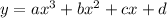
Plug the given points to get four equations

like first point (3,6) gives

`6=a*3^3+b*3^2+c*3+d`

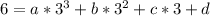
or

`6=27a+9b+3c+d`

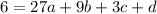
same way we get total four equations:

`6=27a+9b+3c+d, 11=125a+25b+5c+d, 11=64a+16b+4c+d, 21=343a+49b+7c+d`

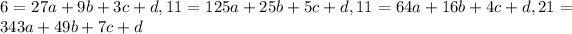
We can solve them to get values of a, b, c and d which are:

`a=(25)/(24), b=-15, c=(1715)/(24), d=-(203)/(2)`

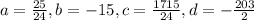
Now plug them into

`y=ax^3+bx^2+cx+d`

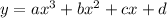
we get required equation as:

`y=(25)/(24)x^3-15x^2+(1715)/(24)x-(203)/(2)`

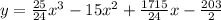
Hence required equation in function notation can be written as

`f(x)=(25)/(24)x^3-15x^2+(1715)/(24)x-(203)/(2)`

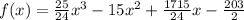
Now to prove that above function is correct, we just graph the given points from table and the obtained function.

We see that points lie on the graph of
`y=(25)/(24)x^3-15x^2+(1715)/(24)x-(203)/(2)`

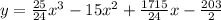
Which proves that our equation is correct.