Question

Using the Rational Root Theorem, name 4 possible roots of the function and show or describe how you found them. f(x) = 5x^3+8x^2−7x−6

Answer 1

Answer: The possible roots are
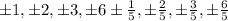`\pm1,\pm2, \pm3,\pm6 \pm(1)/(5),\pm(2)/(5),\pm(3)/(5),\pm(6)/(5)` and the real roots of the function are
`-2,-(3)/(5) ,1`.

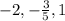Step-by-step explanation:

If a polynomial is defined as,

`p(x)=a_nx^n+a_(n-1)x^(n-1)+...+a_1x+a_0`

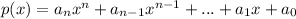
Then all possible rational roots are in the form of,

`r=\pm(p)/(q)`

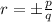
Where p is the factors of
`a_0` and q is the factor of
`a_n`.

The given function is,

`f(x)= 5x^3+8x^2-7x-6`

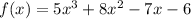
It the given function the constant term is -6 and the leading coefficient is 5.

Factor of -6 are,

`\pm1, \pm2, \pm3,\pm6`

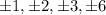
Factors of 5 are,

`\pm1, \pm5`

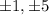
So the all possible rational roots are,

`\pm1,\pm2, \pm3,\pm6 \pm(1)/(5),\pm(2)/(5),\pm(3)/(5),\pm(6)/(5)`

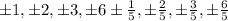
From these value the roots of the function are those values for which the value of the function is 0.

Put all the possible zeros one by one in the function.

Only for
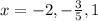`x=-2,-(3)/(5) ,1`, the value of function is 0, so the roots of the function are
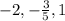`-2,-(3)/(5) ,1`.