Question

Pictures attached.

I'm like 99.9% sure that my inflection point is correct!??

Also, nothing i try for the local extremes is working...

Answer 1

we are given

`f(x)=4x^3+21x^2-294x+7`

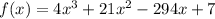
For finding inflection point, we will find second derivative

`f'(x)=4* 3x^2+21* 2x-294+0`

`f'(x)=12x^2+42x-294`

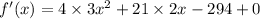
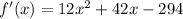
now, we can find derivative again

`f''(x)=12* 2x+42-0`

`f''(x)=24x+42`

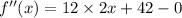
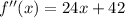
now, we can set it to 0

and then we can solve for x

`f''(x)=24x+42=0`

we get

`x=-(7)/(4)`

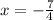
we know that inflection point is a point where concavity changes

so, we will draw a number line and locate x=-7/4

and then we can find sign of second derivative on each interval

Concave up interval:

`(-(7)/(4),\infty)`

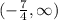
Concave down interval:

`(-\infty,-(7)/(4))`

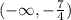
Since, concavity changes at x=-7/4

So, there will be inflection point at x=-7/4

now, we can find y-value

`f(-(7)/(4)) =4(-(7)/(4))^3+21(-(7)/(4))^2-294(-(7)/(4))+7`

`f(-(7)/(4)) =(4515)/(8)`

So, the inflection point is

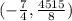`(-(7)/(4),(4515)/(8))`..............Answer