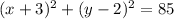Explanation:
Prerequisites:
You need to know:
The distance formula
The standard equation of a circle.
Distance formula:
d =
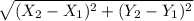
The standard equation of a circle

------------------------------------------------------------------------------------------------------------
First, use the standard equation of the circle and plugin the information we know.
We know the center is (h, k) = (-3, 2)
h = -3
k = 2



Since we do not know our r value, we need to find r. We can find this value by using the distance formula. Remember, the radius (r) is the distance from the center of the circle to a point on the circle. Points we will use are (-3,2) (6,4)
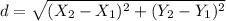

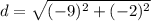
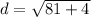
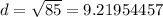
Now we plugin 9.21954457 for r.


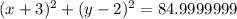
Answer:
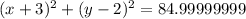
OR