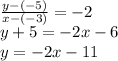Question

Find an equation for the perpendicular bisector of the line segment whose end points are (-9,-8) and (3,-2)

Answer 1

`y=-2x-11`

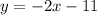
Explanation:

Slope of the line segment = [(-8)-(-2)]/[(-9)-3]=-6/-12=1/2

Slope of the perpendicular bisector x slope of line segment = -1

Slope of perpendicular bisector = -2

Mid-point of line segment = ((-9+3)/2, (-8+(-2))/2) = (-3, -5)

The perpendicular bisector passes through the mid-point.

By point-slope form,

`(y-(-5))/(x-(-3)) = -2\\y+5=-2x-6\\y=-2x-11`