Question

A man finds that the angle of elevationof a building is 22º. After walking 20 m towards the building, he finds that the angle of elevation is 33º. Find the height of the

building?​

Answer 1

The height of the building is 21.38 m

Explanation:

Trigonometric Ratios

The ratios of the sides of a right triangle are called trigonometric ratios.

The image attached shows the measures and angles provided in the problem. The first angle of elevation is y=22°, the man walks B=20 m and finds the new angle of elevation is x=33°.

It's required to find the height of the building H.

The tangent ratio relates the opposite side with the adjacent side of a given angle. Applying it to the larger triangle:

`\displaystyle \tan y=\frac{\text{opposite leg}}{\text{adjacent leg}}`

`\displaystyle \tan 22^\circ=(H)/(D+B)`

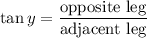
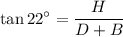
Multiplying by D+B:

`\tan 22^\circ(D+B)=H`

Dividing by tan 22°

`\displaystyle D+B=(H)/(\tan 22^\circ)`

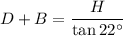
Subtracting B:

`\displaystyle D=(H)/(\tan 22^\circ)-B\qquad\qquad[1]`

Applying to the smaller triangle:

`\displaystyle \tan 33^\circ=(H)/(D)`

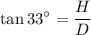
Multiplying by D:

`\tan 33^\circ D=H`

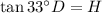
Substituting from [1]:

`\displaystyle \tan 33^\circ \left((H)/(\tan 22^\circ)-B\right)=H`

Substituting values:

`\displaystyle 0.6494 \left((H)/(0.4040)-20\right)=H`

Operating:

`1.6074H-12.988=H`

`1.6074H-H=12.988`

`0.6074H=12.988`

`H = 12.988/0.6074`

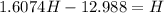
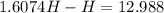
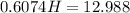
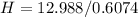
H = 21.38 m

The height of the building is 21.38 m