Question

y = - 1 2 x2 + 2 y = - 3 4 x2 y = - 4 5 x2 - 5 y = -2x2 + 3 For the quadratic equations shown here, which statement is true? A) The graphs open upward. B) The graphs are symmetric about the line x = 1. C) The graphs are listed from narrowest to widest. D) The graphs are symmetric about the y-axis.

Answer 1

\left[y \right] = \left[ 2\,x2\right][y]=[2x2]

Answer 2

D) The graphs are symmetric about the y-axis.

Explanation:

The given equations are

`y=-(1)/(2)x^(2) +2\\y=-(3)/(4) x^(2) \\y=-(4)/(5)x^(2) -5\\y=-2x^(2) +3`

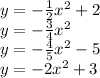
Notice that all given equations have a negative quadratic term.

Remember that the form of a quadratic equation is

`y=ax^(2) +bx+c`

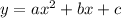
Where
`a` is the coefficient of the quadratic term.

When
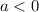`a<0`, the parabola that represents the equation opens downward, because the quadratic term is negative.

Therefore, in this case, the common charactersitc between all equations is that they all represent a parabola which opens downward.

However, there's another characteristic. All parabolas are symmetrical about the y-axis, because the square power has only x-variable inside.

Therefore, the right answer is D.