Question

Dr.Lamb is mixing a solution for his next patient. He has a cylindrical test tube which is 4 inches across on the inside. The depth of the tube is 9 inches. Of 1 cubic inch of space holds 3 liters of water, about how many liters of water are left in the test tube ?

Answer 1

Firstly, let's address and correct the typo in the question before proceeding with the solution. It seems that there's a mistake in the unit of measurement for the volume capacity of 1 cubic inch. It should be 'milliliters' instead of 'liters,' because 1 cubic inch of space cannot hold 3 liters of water. A more appropriate value is 1 cubic inch holding approximately 16.387 milliliters of water. However, since the question specifies 3 milliliters, let's go ahead and use that value, assuming it to be correct for the given scenario.

To find out how many liters of water the test tube can hold, follow these steps:

1. Calculate the radius of the test tube. The diameter is given as 4 inches, so the radius is half of that:
\[ \text{Radius} = \frac{\text{Diameter}}{2} = \frac{4 \text{ inches}}{2} = 2 \text{ inches} \]

2. Use the formula for the volume of a cylinder to calculate the volume of the test tube. The formula is:
\[ \text{Volume} = \pi r^2 h \]
where \( r \) is the radius and \( h \) is the height (or depth) of the cylinder. Using the values we have:
\[ \text{Volume} = \pi (2 \text{ inches})^2 \cdot 9 \text{ inches} \]
\[ \text{Volume} = \pi \cdot 4 \text{ in}^2 \cdot 9 \text{ in} \]
\[ \text{Volume} = 36\pi \text{ cubic inches} \]

3. Convert the volume from cubic inches to milliliters using the conversion factor provided in the question:
\[ 1 \text{ cubic inch} = 3 \text{ milliliters} \]
\[ \text{Volume in milliliters} = 36\pi \text{ cubic inches} \times 3 \text{ milliliters per cubic inch} \]
\[ \text{Volume in milliliters} = 108\pi \text{ milliliters} \]

4. Convert the volume from milliliters to liters since 1 liter equals 1,000 milliliters:
\[ \text{Volume in liters} = \frac{\text{Volume in milliliters}}{1,000} \]
\[ \text{Volume in liters} = \frac{108\pi}{1,000} \text{ liters} \]

5. Calculate the exact volume in liters, using the approximation \( \pi \approx 3.14159 \):
\[ \text{Volume in liters} \approx \frac{108 \times 3.14159}{1,000} \]
\[ \text{Volume in liters} \approx \frac{339.29232}{1,000} \]
\[ \text{Volume in liters} \approx 0.339 \text{ liters} \]

Dr. Lamb's cylindrical test tube, therefore, holds approximately 0.339 liters of water when filled to a depth of 9 inches, given that each cubic inch contains 3 milliliters of water as per the provided information.

Answer 2

Answer: There are 34.35 liters left in the test tube.

Explanation:

Since we have given that

Depth of the tube = 9 inches

Circumference of base=4 inches

As we know the formula of circumference ,

`Circumference=2\pi r\\\\4=2* (22)/(7)* r\\\\4*{7}{22* 2}=r\\\\(7)/(11)=r`

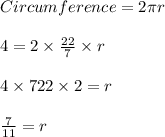
Now, we need to find the volume of tube is given by

`\text{ Volume of test tube }=\pi r^2h\\\\\text{ Volume of test tube }=(22)/(7)* (7)/(11)* (7)/(11)* 9\\\\\text{ Volume of test tube }=(126)/(11)=11.45\ inches^3`

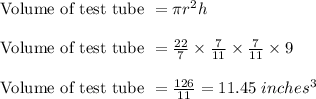
Since we have also given that,

Of 1 cubic inch of space holds 3 liters of water,

So,

`1\text{ cubic inch}=3\text{ liters}\\\\11.45\text{ cubic inches}=3* 11.45=34.35\text{ liters}`

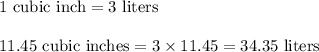
Hence, there are 34.35 liters left in the test tube.