Answer-
The number of waterfowl at the lake on week 8 is 2555
Solution-
Taking
x = input variable = time in week
y = output variable = population of waterfowl
The general best fit equation in Quadratic Regression is,
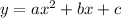
Where,
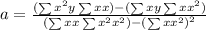
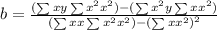
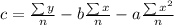
And
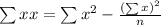
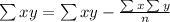

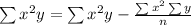
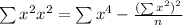
Putting the values in the formula and calculating the values from the table we get,
a = 33, b = -24, c = 635
Therefore, the best fit curve is,
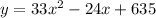
We can calculate the population of waterfowl on 8 week, by putting x = 8

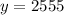
Therefore, the number of waterfowl at the lake on week 8 is 2555.