Question

A biologist took a count of the number of migrating waterfowl at a particular lake and recounted the lake’s population of waterfowl on each of the next six weeks.Find a quadratic function that models the data as a function of x , the number of weeks. Use the model to estimate the number of waterfowl at the lake on week 8

Week

0

1

2

3

4

5

6

Population

635

644

719

860

1,067

1,340

1,679

Answer 1

Answer: the answer is B

Explanation:

Answer 2

The number of waterfowl at the lake on week 8 is 2555

Solution-

Taking

x = input variable = time in week

y = output variable = population of waterfowl

The general best fit equation in Quadratic Regression is,

`y=a x^2 + b x + c`

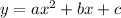
Where,

`a=\frac{(\sum x^2y\sum xx)-(\sum xy\sum xx^2)}{(\sum xx\sum x^2x^2)-({\sum xx^2)}^2}`

`b=\frac{(\sum xy\sum x^2x^2)-(\sum x^2y\sum xx^2)}{(\sum xx\sum x^2x^2)-({\sum xx^2)}^2}`

`c=(\sum y)/(n)-b(\sum x)/(n)-a(\sum x^2)/(n)`

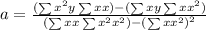
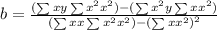
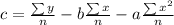
And

`\sum xx=\sum x^2-((\sum x)^2)/(n)`

`\sum xy=\sum xy-(\sum x\sum y)/(n)`

`\sum xx^2=\sum x^3-(\sum x\sum x^2)/(n)`

`\sum x^2y=\sum x^2y-(\sum x^2\sum y)/(n)`

`\sum x^2x^2=\sum x^4-((\sum x^2)^2)/(n)`

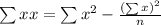
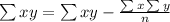
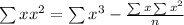
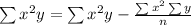
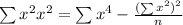
Putting the values in the formula and calculating the values from the table we get,

a = 33, b = -24, c = 635

Therefore, the best fit curve is,

`y= 33x^2-24x+635`

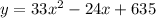
We can calculate the population of waterfowl on 8 week, by putting x = 8

`y= 33(8)^2-24(8)+635`

`y= 2555`

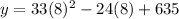
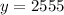
Therefore, the number of waterfowl at the lake on week 8 is 2555.