Question

Put the equation y = x^2 + 26 x + 160 into the form y = ( x − h )^2 + k :

Answer 1

`y = (x + 13)^2 - 9`

Explanation:

To write the given quadratic equation in the form y = ( x − h )^2 + k, we need to complete the square for the given equation.

y = x^2 + 26x + 160

Shift the constant to the left side of the equation:

y - 160 = x^2 + 26x

Divide the coefficient of x by 2 and add the square of the result to both sides of the equation:

26 / 2 = 13

So adding 13^2 to both sides of the equation to get:

y - 160 + (13)^2 = x^2 + 26x + (13)^2

y - 160 + 169 = (x + 13)^2

y + 9 = (x + 13)^2

y = (x + 13)^2 - 9

Answer 2

Put the equation
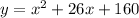`y = x^2 + 26 x + 160` into the form y = ( x − h )^2 + k

Given equation is
`y = x^2 + 26 x + 160`

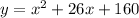
We apply completing the square method

we take coefficient of middle term and then divide by 2 and then square it

coefficient of middle term is 26

Divide by 2, it becomes 13

then we square it (13)^2 = 169

Add and subtract 169

`y = x^2 + 26 x +169 - 169 + 160`

`y = x^2 + 26 x +169 - 9`

`y = (x + 13)^2 - 9`

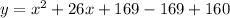
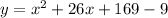
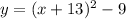
We got the equation in vertex form