Question

((2x^9)(y^n))((4x^2)(y^10))=(8x^11)(y^20)

Answer 1

n = 10

Explanation:

We are given an expression where a power n is unknown.

To find n, we will multiply all the terms at the left side and put them equal to the terms at the right side of the equal sign.

`((2x^9)(y^n)) ((4x^2)(y^(10) )) = (8x^11)(y^20)`

`(2x^9y^n)(4x^2y^(10) ) = 8x^(11) y^(20)`

`8x^(11) y^(n+10) = 8x^(11) y^(20)`

Now this is the most simplified form and we can see the same coefficients on each side so will put n+10 equal to its corresponding value.

`n+10 = 20`

`n = 20-10`

`n = 10`

Answer 2

We are given

`((2x^9)(y^n))((4x^2)(y^(10)))=(8x^(11))(y^(20))`

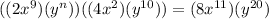
Firstly, we simplify left side

Left side is

`((2x^9)(y^n))((4x^2)(y^(10)))`

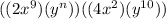
we will make all x terms together

and y terms together

`(2x^9)(4x^2)(y^n)(y^(10))`

`2* 4(x^9)(x^2)(y^n)(y^(10))`

`8(x^9)(x^2)(y^n)(y^(10))`

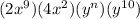
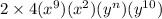
we can multiply left side by using exponent rule

`a^m* a^n=a^(m+n)`

`8(x^(9+2))(y^(n+10))`

`8(x^(11))(y^(n+10))`

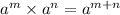
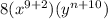
now, we can set them equal

`(8x^(11))(y^(n+10))=(8x^(11))(y^(20))`

Since, both sides have x,y and 8

and both are equal

so, their exponent must be equal

so, exponent of y must also be equal

we get

`n+10=20`

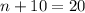
`n=10`................Answer