Question

Which graph represents the solution set of the system of inequalities?

{−2x+y≤4y>x+2

Answer 1

fourth graph

Step-by-step explanation:

Answer 2

The fourth graph is the answer

Step-by-step explanation:

We have inequalities

`-2x+y\leq 4`
`\rightarrow y\leq 2x+4`

`y>x+2`

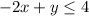
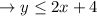
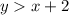
For the first inequality all points at or below the graph of y are solutions, and for the second inequality all the points above the graph of y are the solutions. So, the solution to these inequalities are points that are above the graph of
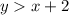`y>x+2` and below the graph of
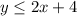`y\leq 2x+4`. The shaded region in the fourth graph satisfies these conditions.

Looking at other choices, we see that the first two graphs do not even represent the graphs of our inequalities, and the third graph does represent the inequalities but shades the wrong region.

P.S: the graph of the inequality
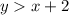`y>x+2` is dashed because
`y` is "greater than" and not "equal to"
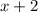`x+2`, so this indicates that the values on the line
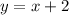`y=x+2` are not included. And the graph of the inequality
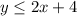`y\leq 2x+4` is a solid line because
`y` is "less than or equal to"
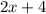`2x+4`, so we are including the values on the line
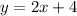`y=2x+4`, and that's why it's solid.