Question

Events A and B are dependent. Find the missing probability.

P(A) = 0.6
P(B\A) = 0.2
P(A and B) = ???

Answer 1

P(A and B) = 0.12

Explanation:

Conditional Probability

Is a measure of the probability of the occurrence of an event, given that another event has already occurred. If event A has occurred, then the probability that event B occurs is given by:

`{\displaystyle P(B\mid A)={\frac {P(B\cap A)}{P(A)}}}`

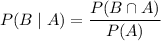
Where
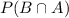`P(B\cap A)` is the probability that both events occur and P(A) is the probability that A occurs.

We are given P(A)=0.6, P(B\mid A)=0.2, and it's required to find P(B\cap A). Solving for the required variable:

`P(B\cap A)=P(B\mid A)*P(A)`

`P(B\cap A)=0.2*0.6=0.12`

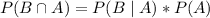
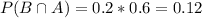
P(A and B) = 0.12