Answer:
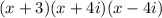 is the required factorization of f(x).
is the required factorization of f(x).
Explanation:
To factor the expression we must first group the terms and then take out common from these groups
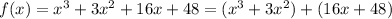
Taking
 common from first group and the 16 from second group we get:
common from first group and the 16 from second group we get:
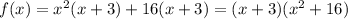
Now, to factor in complex from we have to break term
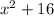
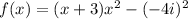
As,
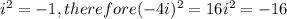
Also using identity
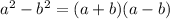
On solving
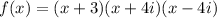
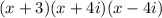 is the required factorization of f(x).
is the required factorization of f(x).