Question

Determine the above sequence converges or diverges. If the sequence converges determine its limit​

Answer 1

This series is convergent. The partial sums of this series converge to
`\displaystyle (2)/(3)`.

Explanation:

The
`n`th partial sum of a series is the sum of its first
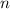`n\!\!` terms. In symbols, if
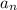`a_n` denote the
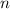`n\!`th term of the original series, the
`\! n`th partial sum of this series would be:

`\begin{aligned} S_n &= \sum\limits_(k = 1)^(n) a_k \\ &= a_1 + a_2 + \cdots + a_(k)\end{aligned}`.

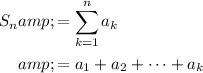A series is convergent if the limit of its partial sums,
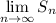`\displaystyle \lim\limits_(n \to \infty) S_(n)`, exists (should be a finite number.)

In this question, the
`n`th term of this original series is:

`\displaystyle a_(n) = \frac{{(-1)}^(n+1)}{{2}^(n)}`.

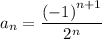The first thing to notice is the
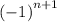`{(-1)}^(n+1)` in the expression for the
`n`th term of this series. Because of this expression, signs of consecutive terms of this series would alternate between positive and negative. This series is considered an alternating series.

One useful property of alternating series is that it would be relatively easy to find out if the series is convergent (in other words, whether
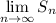`\displaystyle \lim\limits_(n \to \infty) S_(n)` exists.)

If
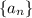`\lbrace a_n \rbrace` is an alternating series (signs of consecutive terms alternate,) it would be convergent (that is: the partial sum limit
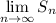`\displaystyle \lim\limits_(n \to \infty) S_(n)` exists) as long as
`\lim\limits_(n \to \infty) |a_(n)| = 0`.

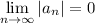For the alternating series in this question, indeed:

`\begin{aligned}\lim\limits_(n \to \infty) |a_n| &= \lim\limits_(n \to \infty) \left|\frac{{(-1)}^(n+1)}{{2}^(n)}\right| = \lim\limits_(n \to \infty) {\left((1)/(2)\right)}^(n) =0\end{aligned}`.

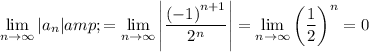Therefore, this series is indeed convergent. However, this conclusion doesn't give the exact value of
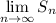`\displaystyle \lim\limits_(n \to \infty) S_(n)`. The exact value of that limit needs to be found in other ways.

Notice that
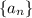`\lbrace a_n \rbrace` is a geometric series with the first term is
`a_0 = (-1)` while the common ratio is
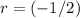`r = (- 1/ 2)`. Apply the formula for the sum of geometric series to find an expression for
`S_n`:

`\begin{aligned}S_n &= (a_0 \cdot \left(1 - r^(n)\right))/(1 - r) \\ &= \frac{\displaystyle (-1) \cdot \left(1 - {(-1 / 2)}^(n)\right)}{1 - (-1/2)} \\ &= \frac{-1 + {(-1 / 2)}^(n)}{3/2} = -(2)/(3) + (2)/(3) \cdot {\left(-(1)/(2)\right)}^(n)\end{aligned}`.

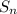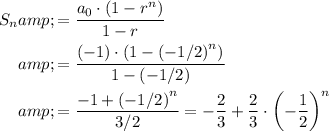Evaluate the limit
`\displaystyle \lim\limits_(n \to \infty) S_(n)`:

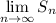`\begin{aligned} \lim\limits_(n \to \infty) S_(n) &= \lim\limits_(n \to \infty) \left(-(2)/(3) + (2)/(3) \cdot {\left(-(1)/(2)\right)}^(n)\right) \\ &= -(2)/(3) + (2)/(3) \cdot \underbrace{\lim\limits_(n \to \infty) \left[{\left(-(1)/(2)\right)}^(n) \right] }_(0)= -(2)/(3)\end{aligned}}_`.

Therefore, the partial sum of this series converges to
`\displaystyle \left(- (2)/(3)\right)`.