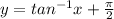Question

Is y=Tan^-1(x+pi/2) the inverse of y=Tan(x-pi/2)? Explain

Answer 1

No.

Explanation:

Here we have our original function as

`y=tan(x-(\pi)/(2))`

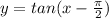
in order to find its inverse , we will replace each x in above equation by y and y with x . And then we solve the new equation for y. LEt us see how :

Given

`y=tan(x-(\pi)/(2))`

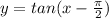
replacing x with y and y with x

`x=tan(y-(\pi)/(2))`

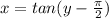
taking tan inverse of x

`tan^(-1)x=y-(\pi)/(2)`

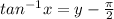
adding
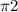`\pi}{2}` on both hand sides

`tan^(-1)x +(\pi)/(2)=y`

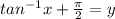
Hence our inverse is

`y=tan^(-1)x +(\pi)/(2)`

Answer 2

Answer: No, the inverse of y is y=tan(x)-pi/2

Solution

y=tan^(-1) (x+pi/2)

Solving for x:

tan(y)=x+pi/2

Subtracting pi/2 both sides of the equation:

tan(y)-pi/2 = x+pi/2-pi/2

tan(y)-pi/2 = x

x=tan(y)-pi/2

Changing x by y and y by x:

y=tan(x)-pi/2