Since, population of species A is represented by :
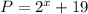
Let us find the population of species A, at the end of week 1:
i.e., x = 1
i.e.,
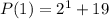
i.e.,
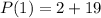
i.e.,
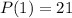
Also, since population of species B is represented by :
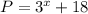
Let us find the population of species B, at the end of week 1:
i.e., x = 1
i.e.,
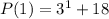
i.e.,
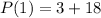
i.e.,
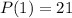
Thus, at the end of 1 week, species A and species B will have the same population.
Hence, option D is correct.