Question

Suppose a parabola has an axis of symmetry at x = -5, a maximum height of 9, and passes through the point (-7,1). write an equation of the parabola in vertex from.

Y = -4(x-5)^2+9
Y = -7(x+9)^2 - 5
Y = -0.06(x-5)^2 + 9
Y = -2(x+5)^2 + 9

Help please...

Answer 1

We are given

a parabola has an axis of symmetry at x = -5, a maximum height of 9

so, we get

vertex =(-5,9)

vertex=(h,k)=(-5,9)

so, h=-5 and k=9

we can use vertex form of parabola

`y=a(x-h)^2+k`

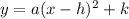
we can plug these value

`y=a(x+5)^2+9`

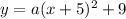
now, it passes through the point (-7,1)

we can use it and then we can solve for a

`1=a(-7+5)^2+9`

`4a+9=1`

`4a=-8`

`a=-2`

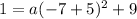
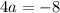
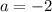
So, we will get equation of parabola as

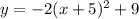`y=-2(x+5)^2+9`..............Answer