Question

How does the graph of g(x)=0.25⌊x⌋ differ from the graph of f(x)=⌊x⌋?

1. Multiplying by 0.25 compresses the graph of ​ ​ g(x)=0.25⌊x⌋ ​ vertically by a factor of 0.25.

2. Multiplying by 0.25 shifts the graph of ​ g(x)=0.25⌊x⌋ ​ ​up 0.25 unit.

3. Multiplying by 0.25 shifts the graph of ​ g(x)=0.25⌊x⌋ ​ right 0.25 unit.

4. Multiplying by 0.25 shifts the graph of ​ g(x)=0.25⌊x⌋ ​down 0.25 unit.

Answer 1

Multiplying by 0.25 compresses the graph of ​ ​g(x)=0.25⌊x⌋​ vertically by a factor of 0.25.

Explanation:

Answer 2

Multiplying by
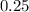`0.25` compresses the graph by a factor a factor of
`0.25`.

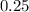EXPLANATION

Given the basic floor function,

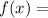`f(x)=`⌊x⌋

We can perform the following transformations,

`f(x)=a`⌊
`x+b`⌋
`+c`.

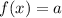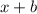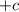The c determines the step-wise y-intercept.

The b determines the horizontal shift

The
`a` tells us the vertical stretch.

If
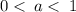`0<\:a<\:1`, the graph compresses vertically by a factor of
`a`.

If
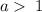`a>\:1`, the graph stretches vertically by a factor of
`a`.

In the diagram, the graph with the color green is the basic function while the graph in the blue color is the vertically compressed function.

You can observe that the steps of the original function are 1 unit above one another while that of the transformed function are 0.25 units above one another.