Question

- 5x2 + 2x + 9= 0
factorize​

Answer 1

Please check the explanation.

Explanation:

Given the quadratic equation

5x²−2x−9 = 0

To factor the quadratic function 5x²−2x−9, we should solve the corresponding quadratic equation 5x²−2x−9 = 0.

Indeed, if x₁ and x₂ are the roots of the quadratic equation ax²+bx+c=0, then

ax²+bx+c = a(x-x₁)(x-x₂)

Now,

solving the quadratic function 5x²−2x−9 = 0

`-5x^2+2x+9=0`

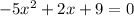
subtract 9 from both sides

`-5x^2+2x+9-9=0-9`

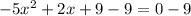
Simplify

`-5x^2+2x=-9`

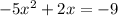
Divide both sides by -5

`(-5x^2+2x)/(-5)=(-9)/(-5)`

`x^2-(2x)/(5)=(9)/(5)`

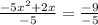
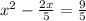
Add (-1/5)² to both sides

`x^2-(2x)/(5)+\left(-(1)/(5)\right)^2=(9)/(5)+\left(-(1)/(5)\right)^2`

`x^2-(2x)/(5)+\left(-(1)/(5)\right)^2=(46)/(25)`

`\left(x-(1)/(5)\right)^2=(46)/(25) \\`

`\mathrm{For\:}f^2\left(x\right)=a\mathrm{\:the\:solutions\:are\:}f\left(x\right)=√(a),\:-√(a)`

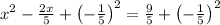
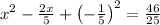
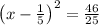
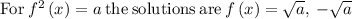
so solving

`x-(1)/(5)=\sqrt{(46)/(25)}`

`x-(1)/(5)=(√(46))/(√(25))`

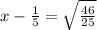
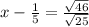
Add 1/5 to both sides

`x-(1)/(5)+(1)/(5)=(√(46))/(5)+(1)/(5)`

`x=(√(46)+1)/(5)`

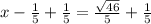
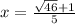
similarly solving

`x-(1)/(5)=-\sqrt{(46)/(25)}`

`x-(1)/(5)=-(√(46))/(5)`

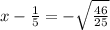
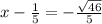
Add 1/5 to both sides

`x-(1)/(5)+(1)/(5)=-(√(46))/(5)+(1)/(5)`

`x=(-√(46)+1)/(5)`

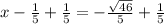
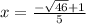
Thus, the roots are:

`x_(1) =(√(46)+1)/(5),\:x_(2)=(-√(46)+1)/(5)`

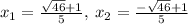
Conclusion:

Since the roots are irrational, we do not factor further.

Therefore, we leave 5x²−2x−9 as it is.