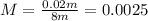Question

Calculate the size of the image of a tree that is 8m high and 80 m a pinhole camera that is 20 cm long . what is its magnification?

Answer 1

1) Size of the image: 2 cm

In order to calculate the size of the image, we can use the following proportion:

`p:q = h_o : h_i`

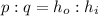
where

p = 80 m is the distance of the tree from the pinhole

q = 20 cm = 0.2 m is the distance of the image from the pinhole

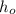`h_o` = 8 m is the heigth of the object

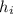`h_i` is the height of the image

By re-arranging the proportion, we find

`h_i = (h_o \cdot q)/(p)=((8 m)(0.2 m))/(80 m)=0.02 m=2 cm`

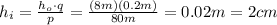
2) Magnification: 0.0025

The magnification of a camera is given by the ratio between the size of the image and the size of the real object:

`M=(h_i)/(h_o)`

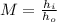
so, in this problem we have

`M=(0.02 m)/(8 m)=0.0025`