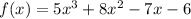ANSWER TO QUESTION 1
Given
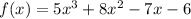
We can use the factor theorem to determine if
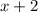 is a factor of the polynomial or not.
is a factor of the polynomial or not.
According to this theorem, if
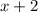 is a factor of
is a factor of
 , then
, then
 .
.
How did we get the
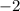 ?
?
We set
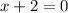 and then solve to obtain
and then solve to obtain
 .
.
So now let us plug in
 in to the function to see if it will simplify to zero.
in to the function to see if it will simplify to zero.
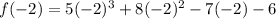
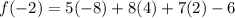
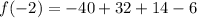
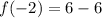

Since the result simplifies to zero, we conclude that
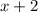 is a factor of
is a factor of
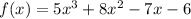
ANSWER TO QUESTION 2
We have the function,
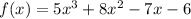
We can use the remainder theorem to show that
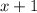 is NOT a factor of the polynomial.
is NOT a factor of the polynomial.
According to this theorem, if
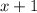 is not a factor of
is not a factor of
 , then
, then
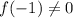 .
.
So now let us plug in
 in to the function to see if it will simplify to non-zero number.
in to the function to see if it will simplify to non-zero number.
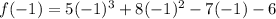
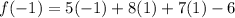
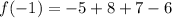
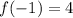
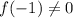
Since the result simplifies to a non zero number, we conclude that
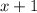 is NOT a factor of
is NOT a factor of