Question

A 480N sphere 40.0cm in radius rolls without slipping 1200cm down a ramp that is inclined at 53 0 with the horizontal. What is the angular speed of the sphere at the bottom of the slope if it starts from rest?

Answer 1

As we know that sphere roll without slipping so there is no loss of energy in this case

so here we can say that total energy is conserved

Initial Kinetic energy + initial potential energy = final kinetic energy + final potential energy

`(1)/(2)mv_i^2 + mgh = (1)/(2)mv^2 + (1)/(2)I\omega^2+ mgh'`

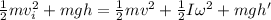
as we know that ball start from rest

`v_i = 0`

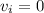
height of the ball initially is given as

`h = Lsin\theta`

`h = 1200sin53 = 960 cm`

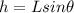
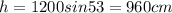
also we know that

`I = (2)/(5)mR^2`

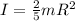
also for pure rolling

`v = r\omega`

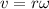
also we know that

`480 = m*9.8`

`m = 49 kg`

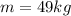
now plug in all data in above equation

`480*9.60 + 0 = (1)/(2)*49*(0.40*\omega)^2 + (1)/(2)*(2)/(5)*49*(0.40)^2\omega^2 + 0`

`4608 = 3.92\omega^2 + 1.568\omega^2`

`\omega^2 = 839.65`

`\omega = 29 rad/s`

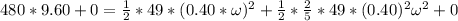
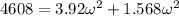
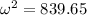
So speed at the bottom of the inclined plane will be 29 rad/s