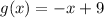Question

The graph of g(x) is the graph of f(x)=x+9 reflected across the y-axis.

Which equation describes function g?

g(x)=x−9

g(x)=−9x+9

g(x)=−x+9

g(x)=−x−9

Answer 1

The equation which describes the function g is:

`g(x)=-x+9`

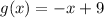
Explanation:

The graph of the function f(x) is given by:

`f(x)=x+9`

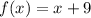
Now, we know that the transformation of the function f(x) when the graph is shifted across the y-axis then it is given by:

f(x) → f(-x)

This means that:

g(x)=f(-x)

i.e.

g(x)= -x+9

Hence, the equation which will represent the graph of the function g(x) is given by:

`g(x)=-x+9`

Answer 2

g(x) = -x +9

Explanation:

Reflecting across the y-axis involves changing the sign of x, so the reflection of f(x) is ...

... g(x) = f(-x) = (-x) +9

The appropriate choice is ...

... g(x) = -x+9