Question

Question 3

<
>
A friend has a 81% average before the final exam for a course. That score includes everything but
the final, which counts for 30% of the course grade.
What is the best course grade your friend cah earn?
%
What is the minimum score would your friend would need on the final to earn a 75% for the course?
%
Give answers accurate to at least one decimal place.
Question Help: D Video Message instructor
Submit Question

Answer 1

The best course grade your friend can earn is 0.867 = 86.7%.

The minimum score would your friend would need on the final to earn a 75% for the course is of 0.61 = 61%.

Explanation:

This is a weighed average problem, in which we multiply each grade by its weight.

We have that:

In 70% of the course, the friend has a grade of 81%.

In the other 30%, he will have x.

What is the best course grade your friend can earn?

This will happen if he earns 100% = 1 on the final test. So

`G = 0.7*0.81 + 0.3*1 = 0.867`

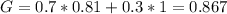
The best course grade your friend can earn is 0.867 = 86.7%.

What is the minimum score would your friend would need on the final to earn a 75% for the course?

This is x, when the grade is 0.75. So

`0.75 = 0.7*0.81 + 0.3x`

`0.3x = 0.75 - 0.7*0.81`

`x = ((0.75 - 0.7*0.81))/(0.3)`

`x = 0.61`

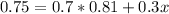
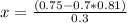
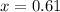
The minimum score would your friend would need on the final to earn a 75% for the course is of 0.61 = 61%.