Question

Two carts (m= 0.4 kg each) are placed on an aluminum track. The first cart pushed with the initial velocity of 1.5 m/s towards the second cart, which remains at rest until the collision. Determine the velocities if both carts after the collision.

Answer 1

here two cars are placed on an aluminium track

so there is no friction on two carts during their motion and hence there is no external force on them

now if there is no external force so momentum is conserved

`m_1v_(1i) + m_2v_(2i) = m_1v_(1f) + m_2v_{2f]`

here

`m_1 = m_2 = 0.4 kg`

`v_(1i) = 1.5 m/s`

`v_(2i) = 0`

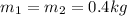
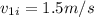
now plug in all values in it

`0.4 * 1.5 + 0 = 0.4* v_(1f) + 0.4*v_(2f)`

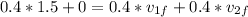
divide whole equation by mass 0.4

`v_(1f) + v_(2f) = 1.5`

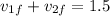
also be the equation of coefficient of restitution

`e = 1 = (v_(2f) - v_(1f))/(v_(1i) - v_(2i))`

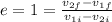
now we have

`v_(2f) - v_(1f) = 1.5`

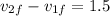
now by solving above equations we will have

`v_(2f) = 1.5 m/s`

`v_(1f) = 0`

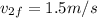
so after collision speed of two carts is 0 m/s and 1.5 m/s after collision