Answer: d. 135 ft
Explanation:
Given: A cell phone tower and post are standing vertical at the same time.
Then they are forming two similar triangles.
We know that the corresponding sides of similar triangles are proportional.
We know that 1 foot = 12 inches.
Then, Height of post =4 ft. 6 in =
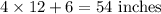
Post's shadow = 3 ft 4 in. =

According to the given question, we have :-

Hence, the height of tower = 135 ft.