Given:
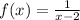
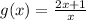
A.)Consider
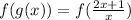
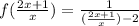
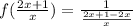
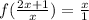
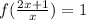
Also,
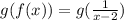

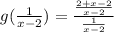
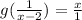
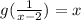
Since,
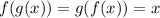
Therefore, both functions are inverses of each other.
B.
For the Composition function
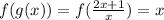
Since, the function
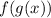 is not defined for
is not defined for
 .
.
Therefore, the domain is
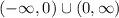
For the Composition function

Since, the function
 is not defined for
is not defined for
 .
.
Therefore, the domain is
