Question

The hypotenuse of a right angled triangle is 2√13 cm . If the smaller side is increased by 2 cm and the larger side is increased by 3 cm , the new hypotenuse will be √117 cm . Find the length of the larger side of the right angled triangle .​

Answer 1

Statement:

The hypotenuse of a right angled triangle is 2√13 cm. If the smaller side is increased by 2 cm and the larger side is increased by 3 cm, the new hypotenuse will be √117 cm.

To find out:

The length of the larger side of the right angled triangle.

Solution:

Let us consider x as the smaller side and y as the larger side.

Then, in the right angled triangle,

x² + y² = (2√13)² ...(I) [By Pythagoras Theorem]

Now, if the smaller side is increased by 2 cm, then the smaller side will be (x + 2).

And if the larger side is increased by 3 cm, then the larger side will be (y + 3).

Then, in the new right angled triangle,

(x + 2)² + (y + 3)² = (√117)² [By Pythagoras Theorem]

or, x² + 2 × 2 × x + 2² + y² + 2 × 3 × y + 3² = (√117)²

or, x² + 4x + 4 + y² + 6y + 9 = (√117)²

or, x² + y² + 4x + 6y + 13 = (√117)²

Now, put the value of x² + y² from equation (I),

or, (2√13)² + 4x + 6y + 13 = (√117)²

or, (2 × 2 × √13 × √13) + 4x + 6y + 13 = (√117 × √117)

or, 52 + 4x + 6y + 13 = 117

or, 4x + 6y = 117 - 52 - 13

or, 4x + 6y = 52

or, 4x = 52 - 6y

or, x =
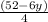`\frac {(52 - 6y)}{4}` ...(II)

Now, put the value of x of equation (II) in (I),

x² + y² = (2√13)²

or,
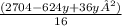`\frac {(2704-624y +36y²)}{16}` + y² = 52

or,
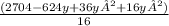`\frac {(2704-624y +36y² + 16y²)}{16}`= 52

or, 52y²-624y + 2704 = 52 × 16

or, 52y² - 624y + 2704 - 832 = 0

or, 52y² - 624y + 1872 = 0

or, 52(y² - 12y + 36) = 0

or, y²-12y +36 = 0 ÷ 52

or, y²-12y +36 = 0

or, (y)² - 2 × 6 × y + (6)² = 0

or, (y - 6)² = 0

or, y - 6=0

or, y = 6

We have taken y as the length of the larger side of the right angled triangle.

So, the length of the larger side is 6 cm.

Answer:

6 cm

Hope you could understand.

If you have any query, feel free to ask.