Question

The path of a softball thrown by maddie forms a parabola wirh the equation y=-3/2401(x-49)^2+8.5 how far does the ball travel vefore it again reaches the same height from which it was thrown

Answer 1

The distance travelled by ball is 98 units before it again reaches the same height from which it was thrown.

Explanation:

The given parabolic equation is

`y=-(3)/(2401)(x-49)^2+8.5`

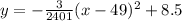
Where, h is height of ball after covering x distance horizontally.

Put x=0, to find initial height of the ball.

`y=-(3)/(2401)(0-49)^2+8.5`

`y=-3+8.5`

`y=5.5`

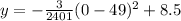
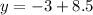
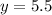
Put y=5.5 in the given equation and find the values of x at which the height of ball is 5.5.

`5.5=-(3)/(2401)(x-49)^2+8.5`

`(3)/(2401)(x-49)^2=-5.5+8.5`

`(3)/(2401)(x-49)^2=3`

`(x-49)^2=2401`

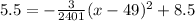
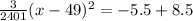
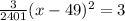
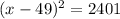
Take square root both sides.

`x-49=\pm 49`

`x=\pm 49+49`

`x=0,98`

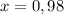
The height of ball is 5.5 at x=0 and x=98.

Therefore distance travelled by ball is 98 units before it again reaches the same height from which it was thrown.