Question

The sum of the three smallest positive values of theta such that 4(cos(theta))(sin(theta)) = 1 is k(pi). Find k.

Answer 1

We are given

`4cos(\theta)sin(\theta)=1`

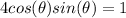
We can divide both sides by 2

`2cos(\theta)sin(\theta)=(1)/(2)`

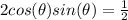
now, we can use trig identity

`2sin(x)cos(x)=sin(2x)`

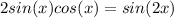
so, we can use it

`sin(2\theta)=(1)/(2)`

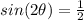
we can take sin^-1 both sides

`2\theta=sin^(-1)((1)/(2) )`

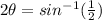
We can take first three positive value

First value is:

`2\theta=(\pi)/(2)`

`\theta=(\pi)/(4)`

Second value is:

`2\theta=(\pi)/(2)+2\pi`

`2\theta=(5\pi)/(2)`

`\theta=(5\pi)/(4)`

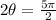
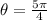
Third value is:

`2\theta=(\pi)/(2)+4\pi`

`2\theta=(9\pi)/(2)`

`\theta=(9\pi)/(4)`

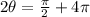
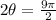
now, we can add them

`\theta=(\pi)/(4)+(5\pi)/(4)+(9\pi)/(4)`

`\theta=(15\pi)/(4)`

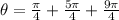
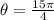
now, we are given that sum is k(pi)

so, we can set them equal

`k\pi=(15\pi)/(4)`

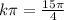
Divide both sides by pi

and we get

`k=(15)/(4)`................Answer