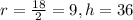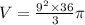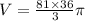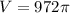Question

Help ASAP!!! Problem is on the picture provided.

Answer 1

Volume of a cone =
`\pi r^2(h)/(3)`

Volume of a sphere =
`(4)/(3) \pi r^3`

Volume of a cylinder =
`\pi r^2h`

With the help of these formulas, we can calculate the volumes.

A cone with a radius of 12 units and a height of 6 units =
`\pi 12^2(6)/(3)` = 288
`\pi`

A sphere with a diameter of 12 units =
`(4)/(3) \pi 6^3` = 288
`\pi`

A sphere with a radius of 9 units =
`(4)/(3) \pi 9^3` = 972
`\pi`

A cylinder with a diameter of 12 units and a height of 27 units =
`\pi 6^227` = 972
`\pi`

A cylinder with a diameter of 8 units and a height of 18 units =
`\pi 4^218` = 288
`\pi`

A cone with a diameter of 18 units and a height of 36 units =
`\pi 9^2(36)/(3)` = 972
`\pi`

Answer 2

QUESTION 1

The volume of a cone is given by;

`V=(\pi r^2h)/(3)`

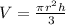
From the given information,

`r=12,h=6`

`V=(12^2* 6)/(3)\pi`

`V=(144 * 6)/(3)\pi`

`V=288\pi`

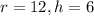
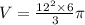
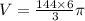
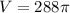
QUESTION 2

The volume of a sphere is given by

`V=(4\pi r^3)/(3)`

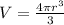
From the given information.\

`r=(Diameter)/(2)= (12)/(2)=6`

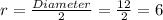
Therefore the volume of the sphere is

`V=(4*6^3)/(3) \pi`

`V=(4*216)/(3) \pi`

`V=288\pi`

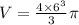
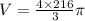
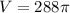
QUESTION 3

The volume of a sphere is given by

`V=(4\pi r^3)/(3)`

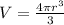
From the given information.\

`r=9`

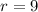
Therefore the volume of the sphere is

`V=(4* 9^3)/(3) \pi`

`V=(4* 729)/(3) \pi`

`V=972\pi`

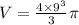
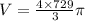
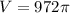
QUESTION 4

The volume of a cylinder is given by

`V=\pi r^2 h`

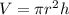
From the given information,

`r=(Diameter)/(2)= (12)/(2)=6`

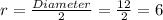
and

`h=27`

Therefore volume of the cylinder

`V=6^2 * 27 \pi`

`V=36 * 27 \pi`

`V=972\pi`

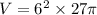
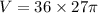
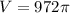
QUESTION 5

The volume of a cylinder is given by

`V=\pi r^2 h`

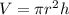
From the given information,

`r=(Diameter)/(2)= (8)/(2)=4`

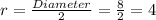
and

`h=18`

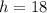
Therefore volume of the cylinder

`V=4^2 * 18 \pi`

`V=16 * 18 \pi`

`V=288\pi`

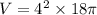
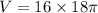
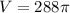
QUESTION 6

The volume of a cone is given by;

`V=(\pi r^2h)/(3)`

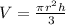
From the given information,

`r=(18)/(2)=9,h=36`

`V=(9^2* 36)/(3)\pi`

`V=(81 * 36)/(3)\pi`

`V=972\pi`